Programming Without Problems
When we talk about programming we can't avoid to talk about problems and how they
can be solved by a program; in particular a computer program.
I think there is a standing feeling that in order to program we require a
problem to solve.
However, certain programs existence is difficult to justify with a problem.
Take for example the ubiquitous Hello World program.
In Oualline's Practical C Programming [1] is laid out on page 13:
[File: hello/hello.c]
#include
int main()
{
printf("Hello World\n");
return (0);
}
For any given program we can craft a suitable problem statement to fulfill the requirement.
In the case of the Hello World program, we can argue the problem is to print
the "Hello World" string followed by a new line on the computer's screen or to
exemplify a simple program.
What about if we craft programs without a specific underlying problem?.
The vast majority of written programs that solve a problem actually describe
how to solve an arbitrary instance of the problem.
It is only when the program is run and the arguments are given that an instance
of the problem is solved.
We can take this even further.
For example, in the Prolog programming language a program consists of predicates
that model facts and rules.
When a program is run, the Prolog's inference engine is asked a goal to
prove and the inference applies unification and backtracking to prove it.
Hence, the problem to solve might not be clear when the rules are being written.
These might be just small semantics nuances, however, I would like to
explore to what extend the problem solving drive, behind writing programs,
has derived in what I call the repetition problem.
Prolog or PROgramming in LOGic is a programming language originated in the
early 1970s.
According to Lloyd [2], before that time logic was regarded only as a
specification language.
The works of Kowalski and Colmerauer seeded the idea that logic can also be used
as a programming language.
Prolog is not fancy in its set of requirements: pattern matching, backtracking
and tree-based data is all it basically needs [3].
A Prolog program is composed of rules and facts [4].
A fact is something that is assumed true under some interpretation, for example
human(alfredo) . On the other hand, a rule is a conditional
mortal(X):-human(X). which is read from right to left:
if x is human then x is mortal.
If you are not familiar with Prolog, I'll explain along the way.
When you load the program into the interpreter, we can ask the query:
mortal(alfredo). and the Prolog interpreter will answer: yes
With this, let us assume we have some facts of the form: d(a,b).
I'm violating a paramount programming rule because d does not stand for
anything, at most it stands for data.
I would like to take a "mathematical approach" and construct logically consistent
rules that may or may not have real-world interpretation.
We can ask if there exists an element A in d's domain such that
it doesn't appear as a right (second) coordinate of any d :
dleft_only(A):-
d(A,_),
\+ d(_,A).
The rule reads, dleft_only(A) is true if there exists a fact such that A is
the first coordinate and there is not (the \+) a fact in which A is
the second coordinate.
The _ indicates we are not interested in the specific value related to
A in d, we are just interested in its existence.
This is also an example of how negation is still addressed in Prolog: it is known
as negation as failure.
The first part of the rule: d(A,_) makes sure that A is in the domain
of d.
The second part \+ d(_,A) can be read as: if you can not prove that
A appears as a second coordinate of a d fact, then succeed.
Likewise we can ask if there is an A in d's domain such that it doesn't
appear as a left (first) coordinate:
dright_only(A):-
d(_,A),
\+ d(A,_).
Using lists we can write more interesting rules.
We can ask if there are walks among the elements of d.
For example, if we have the facts d(1,2). d(2,3). d(3,4).
We would like to know there is a succession of d facts such that if two facts
d(A,B), d(C,D) are together then B and C are the same:
dwalk(A,V,C):-
d(A,C),
;
d(A,B),
\+ member(B,V),
dwalk(B,[B|V],C).
This rule says there is a walk of d's, dwalk, from A
to C
if d(A,C) is a known fact or (the ;) there exists a B such that
d(A,B) is a known fact, we haven't seen B (\+ member(B,V))
and there is a dwalk from B to C.
The list V holds the visited elements.
When we discover a new B we pass it to the recursive call along with V
([B|V]).
We need to keep track of the visited elements to avoid "loops" that could prevent
dwalk from termination.
If we know there are no loops, then we can write a more efficient version:
dwalk(A,C):-
d(A,C)
;
d(A,B),
dwalk(B,C).
We can also write a rule that creates a list of all elements in the in the domain
of d that a given element A can reach:
delems(A,Acc,E):-
d(A,B),
\+ member(B,Acc),
delems(A,[B|Acc],E)
;
d(A,B),
member(B,Acc),
delems(B,Acc,E).
delems(_,Acc,Acc).
In this rule, E will hold all reachable elements.
The first part of the rule (before the ;) adds to the accumulator (Acc),
i.e. to the list of elements we have already discover, any new associate of A.
An associate is new when it is not a member of the Acc list.
If B has not been seen, then a list containing it and all the elements in
the accumulator ([B|Acc]) is passed to the recursive call.
Once all associates are exhausted, the second part explore each associate in turn.
The fact delems(_,Acc,Acc) ensure that when all associations have been exhausted,
the variable E gets unified with the accumulator.
The Prolog engine I use (SICStus Prolog)
evaluates predicates (rules) from top to bottom.
When executing delems, SICStus will try to succeed on the first part and if
it fails, it will try the second part.
However, both parts are written in a way that can be interchanged and still yield
a valid program:
delems_v2(A,Acc,E):-
d(A,B),
member(B,Acc),
delems_v2(A,Acc,E)
;
d(A,B),
\+ member(B,Acc),
delems_v2(B,[B|Acc],E).
delems_v2(_,Acc,Acc).
What changed is only the order in which the d facts are explored.
On the other hand, if we interchange the rules: place delems_v2(_,A,A). before
the other, "no" exploration is performed until explicit backtracks are requested
by the user.
We can find an alternate definition of delems that use rules that we have
defined already.
In our natural language specification of delems, we say any element in the list
E is reachable by A, which is equivalent to: If B is in E after
delems finish, then there exists a dwalk from A to B.
This intuition is supported by the striking resemblance both rules have.
delems_dwalk(A,Acc,E):-
dwalk(A,[A],B),
\+ member(B,Acc),
delems_dwalk(A,[B|Acc],E).
delems_dwalk(_,Acc,Acc).
We can create a rule to calculate a list of all the elements in the domain of
d.
ddomain(Acc,E):-
(d(A,_);dright_only(A)),
\+ member(A,Acc),
ddomain([A|Acc],E).
ddomain(E,E).
ddomain/2 select a left element of a d/2 fact, if it is not in Acc
a recursive call is made passing A along with the elements in Acc.
If the element is in Acc it tries again.
Once the left elements of all d/2 facts are tried, ddomain/2 tries
elements that only appear on the right of d/2 rules.
The /n at the end of a predicate name denotes its arity, it is the standard
way to refer to predicates in Prolog.
So far we have written five rules: dleft_only/1, dright_only/1, dwalk/3,
delems/3, ddomain/2 based on d/2 facts.
They are all correctly specified by their code, that is, their code describes
the functions they calculate.
I will now attempt to specify them at a higher (more mathematical) level of
abstraction and see what we can get.
We'll start with dleft_only/1, dleft_only(A) is true when
.
Where
is the "domain" of d: the set of elements for which
d is defined.
I chose to not write all the quantifiers at the start of the formula just because
I feel this way reads more like an operational specification.
But it is just my personal taste.
dright_only/1 specification is similar: dright_only(A) is true when
.
I summarize all the specifications in the following table
| Predicate | Description |
|---|
| dleft_only/1 | dleft_only(A) is true if
|
| dright_only/1 | dright_only(A) is true if
|
| dwalk/2 | dwalk(A,C) is true if
|
| dwalk/3 | dwalk(A,[A],C) is true if
|
| delems_dwalk/3 | delems_dwalk(A,V,E) is true if
iff
|
| ddomain/2 | ddomain([],E) is true iff
|
I would like to review the previous table.
One of the first things we notice is that we can rewrite d/2 by any other name
e.g. e/2 and the validity of the table holds.
That is, d/2 is kind of a free variable of each rule.
We can factor out d/2 an write an specification for it.
One way to model d/2 is as a binary relation, but this requires us to talk (define)
about domain and codomain which are not exactly present, so far at least,
in our predicates.
Instead let's define d/2 as a sbrelation and every sbrelation is defined
over a finite set of values called its domain and denoted by 𝐃(d).
If two elements a,b in 𝐃(d) are related then we denote it by
d(a,b).
The s in sbrelation comes from static which means that during the execution
of any predicate, the relation can not change, that is, d/2 facts can not be
added nor removed.
We can rewrite the table as follows:
| Predicate | Description |
|---|
| dleft_only/1 |
dleft_only(A) is true if
|
| dright_only/1 |
dright_only(A) is true if
|
| dwalk/2 |
dwalk(A,C) is true if
|
| dwalk/3 |
dwalk(A,[A],C) is true if
|
| delems_dwalk/3 |
delems_dwalk(A,V,E) is true if
iff
|
| ddomain/2 |
∀ d:sbrelation,
ddomain([],E) is true iff
𝐃(d) = E
|
In this new table, is clearer what we mean by d/2, its type of sorts.
Next we can observe, the [A] and [] lists do not play
any role in the specification, only in the implementation:
| Predicate | Description |
|---|
| dleft_only/1 |
∀ d:sbrelation,
dleft_only(A) is true if
A ∈ 𝐃(d) ∧
∃ B ∈ 𝐃(d), d(A,B)∧ ∄ C,
d(C,A)
|
| dright_only/1 |
∀ d:sbrelation,
dright_only(A) is true if
A ∈ 𝐃(d)
∧ ∃ B ∈ 𝐃(d), d(B,A) ∧ ∄
C, d(A,C)
|
| dwalk/2 |
∀ d:sbrelation,
dwalk(A,C) is true if
A, C ∈ 𝐃(d) ∧
(d(A,C) ∨ ∃ B ∈ 𝐃(d), d(A,B) ∧
dwalk(B,C))
|
| delems_dwalk/2 |
∀ d:sbrelation,
delems_dwalk(A,E) is true if
∀ e ∈ 𝐃(d),
dwalk(A,e)
iff
e ∈
E
|
| ddomain/1 |
∀ d:sbrelation,
ddomain(E) is true iff
𝐃(d) = E
|
This new table poses an issue, because what we have implemented dwalk/3,
delems_dwalk/3 and
ddomain/2 is not what it is specified dwalk/2, delems_dwalk/2 and ddomain/1.
We would need to prove that what is implemented meets the specification on the
table.
Let me work out an example, let's take dwalk/3 and sketch a proof for it.
Recall that a walk is a succession of d/2 facts such that if d(A,B),
d(D,C) are together in the succession, then
B = C
.
Let's recall dwalk/3 code:
dwalk(A,V,C):-
d(A,C),
;
d(A,B),
\+ member(B,V),
dwalk(B,[B|V],C).
We can first prove termination of dwalk/3: dwalk(A,[A],C)
terminates
for any
A, C ∈ 𝐃(d)
.
Since the number of d/2 facts is finite we just need to make sure we don't
fall in a loop.
The only execution path that will lead to recursive calls in dwalk/3 is when
a fact d(A,B) is found and B is not already in V.
Since B is added to the contents of V and the new list passed to the recursive
call, then if B is seen again, no recursive call will be made.∎
Then we can prove that
if a call dwalk(D,V,C) is a recursive call with
root call dwalk(A,[A],C), then we can construct an A - D walk with
the elements of V
.
To prove it we proceed by induction on the length of V. If
V = [A,D]
then d(A,D) is a fact; it was added because d(A,D), \+member(D,[A])
succeeded in dwalk/3.
Now, assume that if dwalk(D,V,C) is a recursive call with root call
dwalk(A,[A],C) and the length of V is
l
, then we can construct
an A - D walk with the elements of V.
We will prove if the length of V is
l+1
we can construct an
A - D walk with the elements of V.
In the call dwalk(D,V,C),
V = [D|V']
where V' is a list
of length
l ≥1
.
Let
V' = [B|_]
, then the call dwalk(B,V',C) is a recursive
call with root call d(A,[A],C).
Hence by the induction hypothesis, we can construct an A - B walk.
Since D is in V, d(B,D) is a fact and hence we have constructed
an A - D walk∎.
Now we can prove: Let
A, C ∈ 𝐃(d)
,
dwalk(A,[A],C) succeeds iff there is a walk between
A and C.
First we prove the left-right direction: if dwalk(A,[A],C) succeeds then there
is an A - C walk.
Let dwalk(D,V,C) be the first call that succeeds. That is, d(D,C) is a fact.
By the previous proposition, we can construct an A - C walk.
We now prove the converse: if there is an A - C walk, then dwalk(A,[A],C)
succeeds.
In the left-right direction we showed how to construct an A - C walk,
but this direction only ensures that at least one A - C walk exists.
We haven't characterized walks beyond saying they are a succession of
facts, hence a given walk may have loops.
On the other hand, with our predicate dwalk/3 we can reconstruct walks without
loops, which posses a problem if the only A - C walk contains at least
one loop.
Therefore we must first prove that if an A - C walk contains loops, there
exists an A - C walk that does not.
To achieve this we will only prove that we can remove at least one loop.
Let
w
be an A - C walk that contains at least a loop
L
.
There exists an A - C walk
w'
such that it does not contain
L
.
Let
L = d(X,B),⋯,d(Y,B)
.
If
B = C
then let
w'
be the A - C walk
w
without
L
.
If
B ≠ C
then let d(B,W) the next fact after
L
in
w
.
The walk
w'
defined as the
w
walk removing all facts from
L
but the fact d(X,B) is an A - C walk without the
L
loop∎.
We will prove
if there is an A - C walk, then dwalk(A,[A],C)
succeeds
by contradiction: we will assume dwalk(A,[A],C) fails and that
there exists an A-C walk, then derive a contradiction.
Let
w
be the A-C walk without loops such that
w = A~B,d(B,D),
⋯,d(E,C)
.
Where
A~B
is the longest walk such that the recursive call dwalk(B,V,C)
with root call d(A,[A],C) induces the
A~B
.
Let
NB
be the elements of
𝐃(d)
such that if
X ∈
NB
then d(B,X) is a fact.
Since dwalk(B,V,C) fails, it means it explores all d(B,X) facts, in particular
it will explore d(B,D) which will induce the recursive call dwalk(D,[D,B|V],C)
because
w
does not contains loops.
However, the recursive call dwalk(D,[D,B|V],C) has d(A,[A],C) as root call
and it induces the
A~D
walk wich is longer than
A~B
.
Contradicting our hypothesis about the length of
A~B
∎.
With these results we can be more comfortable with dwalk/3.
Now we can proceed with delems_dwalk/3.
It should not be too difficult to prove delems_dwalk/3 fulfills the delems/dwalk/2
specification because the specification is in terms of the specification of
dwalk/2.
Let's see delems_dwalk/3 definition:
delems_dwalk(A,Acc,E):-
dwalk(A,[A],B),
\+ member(B,Acc),
delems_dwalk(A,[B|Acc],E).
delems_dwalk(_,Acc,Acc).
We just need to prove
e ∈ E
iff dwalk(A,e) succeeds.
The list E gets unified with the list Acc once the first delems_dwalk clause fails.
The first clause fails when any unification of B in dwalk(A,[A],B) is already
a member of Acc.
Now, B in dwalk(A,[A],B) is unified to a domain element iff there is a
walk.
Now we move to justify ddomain/2 with respect to ddomain/1:
ddomain(Acc,E):-
(d(A,_);dright_only(A)),
\+ member(A,Acc),
ddomain([A|Acc],E).
ddomain(E,E).
We must show
ddomain([],E)
=
ddomain(E)
.
First we notice any
B ∈ 𝐃(d)
appears as: left coordinate only,
right coordinate only, both coordinates.
The first part of d(A,_);dright_only(A) will unify A with all possible
left entries.
The elements we miss with the d(A,_) unification are elements that only
appear on the right.
Those unify with dright_only(A).
Hence, any element in the domain of d/2 unifies with A at some point.
When we find an element not in in Acc we continue exploring.
If all elements we find are already in Acc then Acc get unified with E.
The predicate dwalk/3, uses a list to record the history of visited elements.
However, we are only using two operations: membership queries and append-at-head.
We can very well factor this away in a type called sqcontainer which stands
for StackableQueryableContainer and specify dwalk/3 as:
dwalk(A,V,C) is true iff:
∀ d:sbrelation, ∀ V:sqcontainer
A,C ∈ 𝐃(d) ∧ (d(A,C) ∨ ∃ B ∈ 𝐃(d), B ∉ V, d(A,B) ∧ dwalk(B,C))
We can arrange the specifications and predicates we have written so far like in
the following diagram:
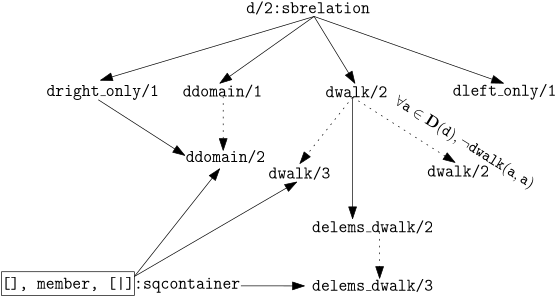
Solid arrows represent direct dependency. Dotted arrows represent implementations.
If a dotted arrow has a label, the label describes the constraints of the implementation.
Dependency shows which specifications are required for a predicate.
For example, delems_dwalk/3 requires access to an sqcontainer and to an
implementation of dwalk/2, which in turns requires d/2 to be defined.
The diagram shows the names of the implementations and of the specifications.
Just as when we defined sbrelation, we can notice names evoke the specification
but they are not the specification.
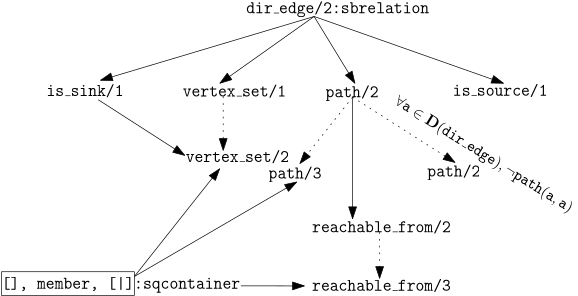
So we can rewrite the names in the diagram and in the specifications table
using any name we wish, for example one of such rewrites could be the following:
| Predicate | Description |
|---|
| is_source/1 |
∀ dir_edge:sbrelation,
is_source(A) is true if
A ∈ 𝐃(dir_edge) ∧
∃ B ∈ 𝐃(dir_edge), dir_edge(A,B)∧ ∄ C,
dir_edge(C,A)
|
| is_sink/1 |
∀ dir_edge:sbrelation,
is_sink(A) is true if
A ∈ 𝐃(dir_edge)
∧ ∃ B ∈ 𝐃(dir_edge), dir_edge(B,A) ∧ ∄
C, dir_edge(A,C)
|
| path/2 |
∀ dir_edge:sbrelation,
path(A,C) is true if
A, C ∈ 𝐃(dir_edge) ∧
(dir_edge(A,C) ∨ ∃ B ∈ 𝐃(dir_edge), dir_edge(A,B) ∧
path(B,C))
|
| reachable_from/2 |
∀ dir_edge:sbrelation,
reachable_from(A,E) is true if
∀ e ∈ 𝐃(dir_edge),
path(A,e)
iff
e ∈
E
|
| vertex_set/1 |
∀ dir_edge:sbrelation,
vertex_set(E) is true iff
𝐃(dir_edge) = E
|
This rewrite change the context dramatically; instead of talking about d/2
facts, we are talking about directed edges, paths, sinks and sources.
We only need to rewrite the predicates we have written so far and we have several
directed graph primitives.
This rewrite is conceptually simple and trivial in a machine, so in principle
we have a method to generate a bunch of meaningful predicates by only rewriting
operations.
Of course we can rewrite the names to anything we want, it is only when
the specification table make sense with respect to the domain we are aiming to
model that the rewrite is meaningful.
It seems there is a way in which we can focus on specifications to describe our domain of interest and relegate source code as a derived, lower-level product.
The rewrite I chose (directed edges and graphs) is tricky because it is a
clean one-to-one correspondence with d/2 universe.
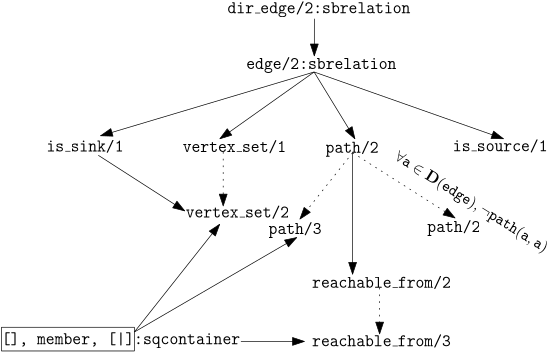
But for example, imagine we define:
edge(A,B):-
dir_edge(A,B)
;
dir_edge(B,A).
And we rewrite the predicates diagram and table of dir_edge/2 (or d/2 it
really doesn't matter which):
| Predicate | Description |
|---|
| is_source/1 |
∀ edge:sbrelation,
is_source(A) is true if
A ∈ 𝐃(edge) ∧
∃ B ∈ 𝐃(edge), edge(A,B)∧ ∄ C,
edge(C,A)
|
| is_sink/1 |
∀ edge:sbrelation,
is_sink(A) is true if
A ∈ 𝐃(edge)
∧ ∃ B ∈ 𝐃(edge), edge(B,A) ∧ ∄
C, edge(A,C)
|
| path/2 |
∀ edge:sbrelation,
path(A,C) is true if
A, C ∈ 𝐃(edge) ∧
(edge(A,C) ∨ ∃ B ∈ 𝐃(edge), edge(A,B) ∧
path(B,C))
|
| reachable_from/2 |
∀ edge:sbrelation,
reachable_from(A,E) is true if
∀ e ∈ 𝐃(edge),
path(A,e)
iff
e ∈
E
|
| vertex_set/1 |
∀ edge:sbrelation,
vertex_set(E) is true iff
𝐃(edge) = E
|
Intuitively by the new context, graphs, we "know" it makes no sense to talk about
sources and sinks because with edge/2 we removed any sense of direction.
An approach in which we can not 'deduce' it without having to write tests would
not be too useful.
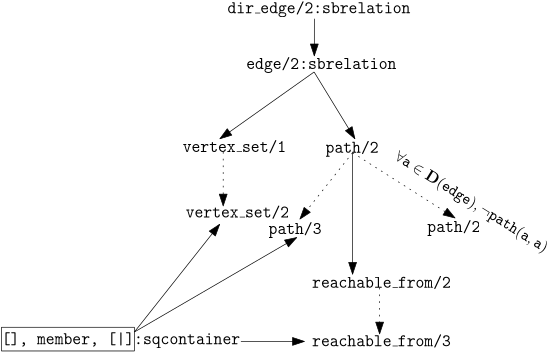
However, by looking at the specifications, we can easily tell both is_source/1
and is_sink/1 will always be false; the first part of both definitions
is for the existence of edge(A,B) in the is_source/1 case and edge(B,A)
in the is_sink/1 case.
However, edge/2 ensures that edge(A,B) is true iff edge(B,A).
And hence, we would not be able to satisfy
∄ C, edge(C,A)
nor
∄ C, edge(A,C)
.
This observation induces simplifications:
| Predicate | Description |
|---|
| path/2 |
∀ edge:sbrelation,
path(A,C) is true if
A, C ∈ 𝐃(edge) ∧
(edge(A,C) ∨ ∃ B ∈ 𝐃(edge), edge(A,B) ∧
path(B,C))
|
| reachable_from/2 |
∀ edge:sbrelation,
reachable_from(A,E) is true if
∀ e ∈ 𝐃(edge),
path(A,e)
iff
e ∈
E
|
| vertex_set/1 |
∀ edge:sbrelation,
vertex_set(E) is true iff
𝐃(edge) = E
|
In particular vertex_set/2 code is modified to:
vertex_set(Acc,E):-
d(A,_),
\+ member(A,Acc),
vertex_set([A|Acc],E).
vertex_set(E,E).
Up to this point all we have done is rewriting operations and removal of
unsatisfiable predicates (dead-code of sorts).
Now, let us write some predicates under this new interpretation.
We can write a predicate to find the "degree" of a vertex, that is, the number
of neighbors in the graph of a vertex:
degree(V,D):-
degree(V,[],D).
degree(V,Acc,D):-
edge(V,U),
\+member(U,Acc),
degree(V,[U|Acc],D).
degree(V,Acc,D):-
length(Acc,D).
We can specify degree/2 as: Let
V ∈ 𝐃(edge), N ⊆𝐃(edge)
such that
∀ n ∈ N, edge(V,n)
is true and vice-versa.
degree(V,D) is true iff D is the cardinality of
N
.
I won't sketch the proof as I want to focus on the question: is there an interpretation
of degree/2 that makes sense in the d/2 'universe'?
The intuitive answer is yes.
How can we go about it?
We can do a "direct" rewrite of the specification edge/2 by d/2 and it
would yield the following:
Let
V ∈ 𝐃(d), N ⊆𝐃(d)
such that
∀ n ∈ N, d(V,n)
is true and vice-versa.
degree(V,D) is true iff D is the cardinality of
N
.
We can also do a "guided" rewrite: edge/2 is defined in terms of dir_edge/2
that is, edge/2 was not a direct rewrite of dir_edge/2 but dir_edge/2
was a direct rewrite of d/2.
A "guided" rewrite, rewrites a specification by its definition, this would yield:
Let
V ∈ 𝐃(d), N ⊆𝐃(d)
such that
∀ n ∈ N, d(V,n);d(n,V)
is true and vice-versa.
degree(V,D) is true iff D is the cardinality of
N
.
Both specifications are, as expected, different.
The first specification in terms of d/2 could be read by an d/2 expert probably
as the left degree.
While the second specification could be read as the degree.
The rewrites performed from d/2 to edge/2 are not extremely complicated
and so, it is easy to come up with three new specifications and the respective
code:
| Predicate | Description |
|---|
| dleft_degree/2 | Let
V ∈ 𝐃(d), N ⊆𝐃(d)
such that
∀ n ∈ N, d(V,n)
is true and vice-versa. dleft_degree(V,D) is true iff D is the cardinality of
N
|
| dright_degree/2 | Let
V ∈ 𝐃(d), N ⊆𝐃(d)
such that
∀ n ∈ N, d(n,V)
is true and vice-versa. dright_degree(V,D) is true iff D is the cardinality of
N
. |
| ddegree/2 | Let
V ∈ 𝐃(d), N ⊆𝐃(d)
such that
∀ n ∈ N, d(n,V);d(V,n)
is true and vice-versa. ddegree(V,D) is true iff D is the cardinality of
N
. |
dleft_degree(V,D):-
dleft_degree(V,[],D).
dleft_degree(V,Acc,D):-
d(V,U),
\+member(U,Acc),
dleft_degree(V,[U|Acc],D).
dleft_degree(V,Acc,D):-
length(Acc,D).
dright_degree(V,D):-
dright_degree(V,[],D).
dright_degree(V,Acc,D):-
d(U,V),
\+member(U,Acc),
dright_degree(V,[U|Acc],D).
dright_degree(V,Acc,D):-
length(Acc,D).
ddegree(V,D):-
ddegree(V,[],D).
ddegree(V,Acc,D):-
(d(U,V);d(V,U)),
\+member(U,Acc),
ddegree(V,[U|Acc],D).
ddegree(V,Acc,D):-
length(Acc,D).
It is evident that we can make some optimizations, like join both predicates
that unify D.
For now, let us focus only on this kind of correct copy-paste-rewrite
procedure.
We have shown that this model is flexible enough to allow specifications to
flow bidirectionally:
If we create an specification in a derived model,it is possible to interpret the new specification on the root model
.
This property promotes code-reuse in a broader way than libraries, for example.
Libraries are functionality providers, unless we have access to the library's source
code and a working knowledge of its internals, it is almost impossible to grow
their capabilities (with some exceptions like Objective-C's decorators).
I want to take a closer look at dwalk/3 and its specification dwalk/2.
In particular to the proposition:
if a call dwalk(D,V,C) is a recursive call with
root call dwalk(A,[A],C), then we can construct an A - D walk with
the elements of V
.
A key element of this proposition is the root call hypothesis: dwalk(A,[A],C).
It allows us to reconstruct the A - D walk by induction.
Moreover, the rest of the proofs also make the root call hypothesis.
Which raises the question: What about if dwalk(A,[A],C) is not the root call?
This kind of questions often arise during programming and are possible bug spots
because the intended use do not match the possible uses.
When I introduced dwalk/3 I said the list V in dwalk(A,V,C)
holds the visited elements and through the reasoning of the proofs and the text
that is certainly the case.
However, that happens if the root call is dwalk(A,[A],C).
So, what does dwalk(A,V,C) actually do?
We can try to think about specific calls, e.g. dwalk(A,[],C), dwalk(A,[B],C),
dwalk(A,[A],A), etc. And attempt to come up with an specification.
One thing is clear, whatever the specification we derive, an special case is
dwalk(A,[A],C) is true iff dwalk(A,C).
But, as we will see, there is a bit more to it.
First we notice dwalk/3 succeeds iff d(X,Y) and dwalk(X,_,Y)
is a recursive call, including a root call.
If a call dwalk(A,V,C) is made such that d(A,C) is not a fact, then
a B is search in the database such that d(A,B) is a fact.
Once a candidate is found, then we check if B is not in V.
Now, V is not constrained, so, if in the root call it contains a non empty
list of elements, those will be excluded from the search.
Hence, the actual role of V is to be an
exclusion list
.
Each time an element B not in V is selected, it is added to the exclusion
list for the remaining of the computation.
This observation certainly opens up the possibility for new predicates.
Now we should write an specification for dwalk/3 that makes makes V's
role explicit:
| Predicate | Description |
|---|
| dwalk/3 |
∀ d:sbrelation,
dwalk(A,V,C) is true if
A, C ∈ 𝐃(d) ∧
(d(A,C) ∨ ∃ B ∈ 𝐃(d), d(A,B) ∧
B ∉ V ∧ dwalk(B,[B|V],C))
|
I chose Prolog for this experiment because of its powerful unification, backtracking
and its broader type system.
It allows to write programs closer to my intended specifications.
With another language, it would have been a bit cumbersome to create all the
scaffolding required to start writing the first functions.
[1] Oualline S., "Practical C Programming", 3rd ed, O'Reilly, 1997.
[2] Lloyd, J. W., "Foundations of Logic Programming",
Springer-Verlag, 1984.
[3] Bratko, I., "Prolog programming for artificial intelligence",
Addison-Wesley, 3rd ed., 2001.
[4] Gersting, J. L., "Mathematical Structures for Computer
Science", W. H. Freeman and Company, 3rd printing, 1999.
Copyright Alfredo Cruz-Carlon, 2025



