ACCorner: PWPIV

Programming Without Problems IV: A map example

Caesar cipher

As part of the predicates we have developed so far for d/2 facts we have dfunction/0 and dmap/0 that are true if the d/2 relation is a function (dfunction/0) or a biyective function (dmap/0). Unlike the previous entries of this series, I would like to see how we can apply dmap/0 to a simple problem, so I chose Caesar cipher.
In a nutshell Caesar cipher encodes a text by shifting each letter a pre-defined number of places, for example, in the following figure the letters in the smallest polygon are shifted three places to the right with respect to the letters on the outer polygon:

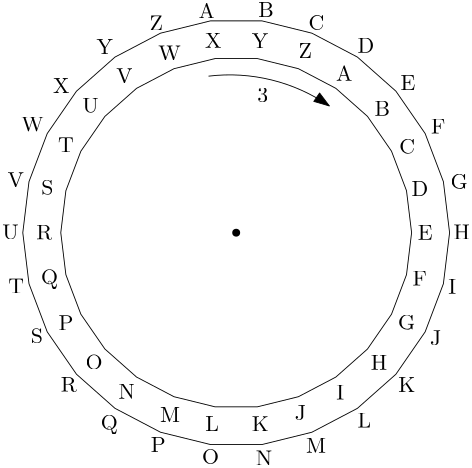
So, if we write the message "HELLO WORLD" using the alphabet in the inner polygon, it would be encoded using the outer polygon as: "KHOOR ZRULG". To simulate the polygon in a program we first define a map between an alphabet and an index set:


         alph(a,14).
         alph(b,15).
         alph(c,16).
         alph(d,17).
         alph(e,18).
         alph(f,19).
         alph(g,20).
         alph(h,21).
         alph(i,22).
         alph(j,23).
         alph(k,24).
         alph(l,25).
         alph(m,0).
         alph(n,1).
         alph(o,2).
         alph(p,3).
         alph(q,4).
         alph(r,5).
         alph(s,6).
         alph(t,7).
         alph(u,8).
         alph(v,9).
         alph(w,10).
         alph(x,11).
         alph(y,12).
         alph(z,13).

How are we sure that alph/2 is a map? Well, we can inspect it manually, but we have seen how that sometimes turns out. Another possibility is to rewrite dmap/0 to work with alph/2 instead of d/2. The only problem is that dmap/0 depends on predicates that depend on other predicates that depend on d/2 predicates (see here for a dependency graph) so a manual rewrite could be even more error-prone than a manual check. To avoid these problems, and the boredom of manual rewrite, I wrote a small Python scrip to rudimentary parse all the predicates we have written so far, calculate dependencies and rewrite. The generated program looks like:


         /*********************************************************
         Code generated by rewriter.py
         Base filename: d.pl
         d/2 ---> alph/2
         dmap/0 ---> alphmap/0
         *********************************************************/
         :- use_module(library(lists)).
         :- use_module(library(aggregate)).
         :- consult(encoder).
         % Required predicate
         alph_ddomain_left(Acc,LD):-
         	alph(A,_),
         	\+member(A,Acc),
         	alph_ddomain_left([A|Acc],LD).
         alph_ddomain_left(LD,LD):-
         	forall(member(B,LD),alph(B,_)),
         	forall(alph(B,_),member(B,LD)).
         % Required predicate
         alph_ddomain_left(LD):-
         	alph_ddomain_left([],LD),!.
         % Required predicate
         alph_ddomain_right(Acc,RD):-
         	alph(_,A),
         	\+member(A,Acc),
         	alph_ddomain_right([A|Acc],RD).
         alph_ddomain_right(RD,RD):-
         	forall(member(B,RD),alph(_,B)),
         	forall(alph(_,B),member(B,RD)).
         % Required predicate
         alph_ddomain_right(RD):-
         	alph_ddomain_right([],RD),!.
         % Required predicate
         alph_dleft_neighbors(A,Acc,Ln):-
         	alph(A,B),
         	\+member(B,Acc),
         	alph_dleft_neighbors(A,[B|Acc],Ln).
         alph_dleft_neighbors(A,Ln,Ln):-
         	forall(member(B,Ln),alph(A,B)),
         	\+((alph(A,C), \+member(C,Ln))).
         % Required predicate
         alph_dleft_degree(A,D):-
         	alph_dleft_neighbors(A,[],Ln),
         	length(Ln,D).
         % Required predicate
         alph_dright_neighbors(B,Acc,Rn):-
         	alph(A,B),
         	\+member(A,Acc),
         	alph_dright_neighbors(B,[A|Acc],Rn).
         alph_dright_neighbors(B,Rn,Rn):-
         	forall(member(A,Rn),alph(A,B)),
         	\+((alph(C,B), \+member(C,Rn))).
         % Required predicate
         alph_dright_neighbors(B,Rn):-
         	alph_dright_neighbors(B,[],Rn),!.
         % Required predicate
         alph_dright_degree(B,D):-
         	alph_dright_neighbors(B,Rn),
         	length(Rn,D).
         % Required predicate
         alph_dfunction:-
         	alph_ddomain_left(LD),
         	forall(member(X,LD),alph_dleft_degree(X,1)).
         % Rewritten predicate
         alphmap:-
         	alph_dfunction,
         	alph_ddomain_right(RD),
         	forall(member(Y,RD),alph_dright_degree(Y,1)).

The file encoder.pl contains the definition of alph/2. If we load this program and query alphmap it would succeed. So we can be sure that alph/2 is a map and we can move on. The next step is to define shifts, for example we can simulate the two wheels in the figure with the predicate:


         enc(A,B):-
         	alph(A,N),
         	I is N + 3,
         	TI is mod(I,26),
         	alph(B,TI).

Which we can read as A is encoded as B iff $N, TI are the indicesof A and B \land N + 3 \equiv TI (mod 26)$ . For enc/2 to be correct, it must be a map, so, we can synthesize a version of dmap/0 rewritten for enc/2 and execute it. What might be curious is how the decode is calculated. Unlike the traditional approach in which the decode is implemented, enc/2 relies on backtrack: if B is given but A is not, then it tries all possible values until the correct value is found. So far, we have used the rewrites to verify that we created maps, but imagine we make a mistake and instead we write:


         enc(A,B):-
         	alph(A,N),
         	I is N + 3,
         	TI is mod(I,25),
         	alph(B,TI).

If we run the program again, then Prolog would be unable to proof enc/2 is a map, however, it would only say no and would not elaborate further. This is annoying because, how many times have you yelled at your computer: why, why don't you work? . It would certainly be nice if we could get a counter-example, kind of: this is wrong because it doesn't work here ... . It seems to be a good idea to write a counter-example finder for dfunction/0 and dmap/0:


         dfunction_ce(CE):-
         	ddomain_left(LD),
         	member(X,LD),
         	dleft_degree(X,Ld),
         	Ld =\= 1,
         	dleft_neighbors(X,LNeigh),
         	CE = (X,LNeigh).
         
         dmap_ce(CE):-
         	dfunction_ce(CE)
         	;
         	ddomain_right(RD),
         	member(Y,RD),
         	dright_degree(Y,Rd),
         	Rd =\= 1,
         	dright_neighbors(Y,Rneigh),
         	CE = (Y,Rneigh).

If we rewrite dmap_ce/1 to work with enc/2 then Prolog would give us conter-example and help us debugging the problem. dmap_ce/1 and dfunction_ce/1 can also be used to help create functions and maps by incrementally detecting which cases need to be refined.

It would be nice to be able to ensure that enc/2 is a map without having to calculate its domain, the way dmap/0 does. And it would be even nicer if we could ensure this behavior by design , for example to define enc/2 as a composition of maps:


         enc(A,B):-
         	alph(A,N),
         	//alph/2 is a map
         	//ddomain_left == [0,...,25]
         	I is N + 3,
         	//(+ 3)[0,...,25] defines the map [0,...,25] -> [3,...,28]
         	TI is mod(I,26),
         	//(mod 26) defines the map [3,...,28] -> [0,...,25]
         	alph(B,TI).
         	//alph/2 is a map
         	//ddomain_left == [0,...,25]
         	//therefore: enc/2 define a map [0,...,25] -> [0,...,25]

With what we have developed so far, we can not perform these kind of symbolic reasoning, we are on the phase of generating code automatically that have some correctness guarantees, but it seems that if we had + and mod functions specified in our table we could achieve enc/2 as a composition and rewrite operation, could this work?