ACCorner: PWPIV.1

Programming Without Problems IV.1: The Bit that Matters the Most

MSB

In the last Programming Without Problems (PWP), we used rewrite to implement Caesar cipher by modeling the alphabets as maps (map/0) and hinted about going forward in this direction. The spoiler is that PPW V is planned to explore off-by-one errors, but to do that I need a tool to reason about lengths symbolically which can not happen kind of easy within the d/2 universe, so I'm working on that. However, while I was browsing X I came across this post:

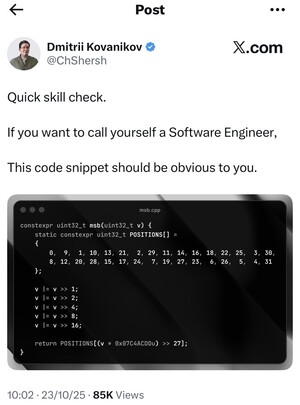
I think it exemplifies quite nicely the point I try to convey with the PWP series: All the expertise required to write the code is confined to the author and the people that understands it deeply enough to adapt the techniques used to other settings. I think it is highly probable that techniques get lost or rediscovered over and over again; to adapt something from a domain into another usually means you must be well versed on both domains, however, the idea behind PWP is to be able to get working and correct code by only focusing on expressing ideas in the domain of your choosing. I won't dwell into its obviousness and how it correlates with your (my) ability to call yourself (myself) a Software Engineer. History has showed that for any given subject there are at least two sets of people: those that understand it without explanation and those that understand it after an explanation, take the history of the concept of zero as an example.

At first I was like.. "wtf does this do?" and then I saw the name of the file: msb.cpp and I was like: "am I thinking about the same bit?, you know the 1 bit that if you read the binary representation from left to right is the first you encounter?" The POSITIONS array caught my eye, it looked a bit strange, why is it for 32 bits unsigned integers when the highest value is 31 and arranged in such a strange way? Then was that constant 0x07C4ACDD and the multiplication. I could see myself trying to write that code and being worried all the time asking myself "did I get the order right?". What about if I messed up and shift A for C in the constant or misplace a number in the POSITIONS array? We can argue this piece of code might be easy to test, however, wouldn't be better if we wouldn't need to test it in the first place? Besides, this is the kind of code in which the compiler would not help you at all. So, of course, I asked myself: "Hmm could it be possible to derive this automatically from a higher level of abstraction in such a way the design elements can be reused?"

Dissection

In order to start talking about the Most Significant Bit (msb) and the mentioned code in the PWP philosophy we need to specify the msb in a higher-level of abstraction. Let us define the relation UInt that models a binary representation of an unsigned integer. The left-domain of UInt would be the range $[0...n-1]$ and the right-domain would be $[0, 1]$ . We can characterize the msb as: UInt(i,1) is the msb iff $\forall UInt(m,1), i \geq m$ . We can also assume a canonical model of a 32 bit integer variable var as: x = var&0x00000001 iff UInt(1,x), x = var&0x00000002 iff UInt(2,x), and so on. Let me paste the code so we don't have to zoom in the picture:


         constexpr uint32_t msb(uint32_t v){
             static constexpr uint32_t POSITIONS[] =
             {
                 0,  9,  1, 10, 13, 21,  2, 29, 11, 14, 16, 18, 22, 25,  3, 30,
         	 8, 12, 20, 28, 15, 17, 24,  7, 19, 27, 23,  6, 26,  5,  4, 31
             };
         
             v |= v >> 1;
             v |= v >> 2;
             v |= v >> 4;
             v |= v >> 8;
             v |= v >> 16;
         
             return POSITIONS[(v * 0x07C4ACDDu) >> 27];
         }

Our first goal is to make sure the code fulfills the specification. For that we will dissect it and abstract some of our observations. Let's assume the msb is at bit i. The instruction v >> 1 will 'shift' the msb from the position i into the position i-1. Hence, the instruction v |= v >> 1 will copy the msb into v at the i-1 position. The instruction v >> 2 shifts the msb and its copy into the position i-2. An so v |= v >> 2 copies the msb and its copy at the bits i-2, i-3 respectively. What we can take away from this pattern is: If we need to propagate the top m bits we can do it as v |= v >> m, v |= v >> 2*m and so on. This should work on 'bigger' constructs, as long as some preconditions hold, like neutral filled to the left and etc.

After the execution of v |= v >> 16 the variable v has the lowest i+1 bits set to 1 and the rest set to 0. We can observe that both numbers, the original value of the argument v and the new value have the same msb. If the number of on bits on the new value of v is not zero then it is exactly the msb plus 1. At this point we can use various approaches, count the number of 1's, count the number of consecutive 1's or subtract from 32 the number of leading zeros; but this last approach we can apply without having to do the shifts and or's. Now we need a way to map any given number of the form $0$ ^m1ⁱ where $m + i = n$ to the interval $[0, ..., n-1]$ . In the code, POSITIONS is a map, we can use a rewrite of d/2 to make sure if we don't believe our eyes. So the expression POSITIONS[(v * 0x07C4ACDDu) >> 27] must be a composition of maps and (v * 0x07C4ACDDu) >> 27 must be the map we are searching. The expression (v * 0x07C4ACDDu) >> 27 discards the 27 least significant bits, leaving the 5 most significant bits untouched, which are the necessary bits to express a number in the interval $[0, ..., 31]$ . So, it would be nice to check that the five most significant bits of the product v * 0x07C4ACDDu represent a map regardless of the value of v i.e. that it is a reversible function. We know that there are 32 different values of v so we can perform the 32 multiplications and check if the 5 most significant bits of the result make a map, but then we would be wondering how 0x07C4ACDD came to be and why a multiplication.

We know from elementary school that for any two given natural numbers $a, b$ , $a * b = b + b + ... + b$ where the number of $b$ 's is exactly $a$ . So, at first glance, v may not be a small number, and 0x07C4ACDD does not look like a small number either, so the multiplication might not be small either. However, we can simplify this particular multiplication because of v's value shape: $0$ ^m1ⁱ . Let's assume v's value is not zero, so the leftmost bit is 1 hence we have a copy of 0x07C4ACDD. If v's value is greater than 1 then we need to add our copy of 0x07C4ACDD with itself but shifted to the left by one and so on. So, is 0x07C4ACDD the only number that $\sum_{j=0}^{i} 0x07C4ACDD << j$ makes such a map? If the sum is familiar, it might be because you recall the front cover of Warren's book:

I tried to find another number by hand following no particular strategy (including no Wikipedia) with no success. By the time I filled two sheets of paper I was double and triple checking my work, I knew I had to find another 'error-free' approach. So I decided to try a "greedy" approach, from a seed (a left-to-right prefix of bytes) try to find the rest bytes keeping the candidate that has the biggest map. This approach found a few numbers but I could still not see an obvious (to me) closed formula however, it answered my question, 0x07C4ACDD is not unique. Having my attention split between the game 2 of the World Series and this, I yielded and decided to try a brute force attack, after all it is not the 00's and you can explore the whole 32 bit range quite rapidly now. After 10 minutes, the program generated a list of all possible magic numbers, you can consult it here. There are 1024 numbers and 0x07C4ACDD is the smallest of them. The next question is, how many of the induced maps are different? It turns out each magic number induces its own map which is kinda cool. You can consult the maps here. There is a caveat tho: If you look closely at the maps, you will find they use 0 as a possible map value including the original 0x07C4ACDD. If we happen to use any of these maps in the msb code, we would need to detect when the argument is 0 or be sure that 0 would not be an argument.

The elements

I think the techniques used in the code, should be specified in d/2 universe, or more probably in some variation of it. The magic numbers counting can be generalized, there is no restriction on the number of bits used for the map nor their physical location, so, there is room to generalize magic numbers and magic maps. The code that wrote the magic tables can be changed to synthesize programs that count consecutive low 1 bits. Any technique that requires to count consecutive low 1 bits then just need to synthesize the code and move on. Personally I loved this MSB detection approach specially because behind the multiplication there are a bunch of (conceptual) additions that happen to be faster than using a fix number of high level additions, bit shifts and masks.

To de Bruijn or not to de Bruijn

Among some comments to the post there were a some calling this a "nice de Bruijn trick" but that it should not be used in production code. I have a problem when people call things "a trick" because the definition of a trick is to mislead or outwit. And if anything there is no trick here, it is just a property but I completely understand the feeling you would get if you encounter it as part of a code you need to work on, after all you do not use to document what you consider obvious . To me it is a clear sign that, sometimes, source code is too low level to convey high level ideas and we should raise our level of abstraction not only our level of "source code documentation". On the other hand, this kind of justifications to not use a piece of code seem naive, it would be like saying you don't use an assembly instruction because you don't understand its schematics. Again we should be focusing on raising our level of abstraction.

The "de Bruijn" part is interesting, because if you look into Wikipedia it would show a striking similar version using a de Bruijn sequence. The question is: are the magic numbers de Bruijn sequences? A de Bruijn sequence of order 5 on a binary alphabet must contain all possible 5 bit strings as sub-strings exactly once. 0x07C4ACDD is a de Bruijn sequence but the magic number 0xF83B5323 is not (as far as I can tell) and the de Bruijn number 0x06EB14F9 is not a magic number (see Appendix). The fact that 0x07C4ACDD is a de Bruijn sequence is a nice coincidence, actually only 768 magic numbers out of 1024 are not de Bruijn. This also highlights the need to look into the seemingly obvious because this kind of bugs can also appear even in what I'm suggesting at PWP. The scenario would be: we have the misconception that this particular approach involves using a de Bruijn map and generate any map just to later find out our supposedly correct code is completely wrong.

Incomplete

The code is slightly incomplete, if v is 0 or v is 1 then asnwer is the same: 0. If not used with "care" then an user could conclude the msb of 0 is at bit 0. Of course the standard solution is to restrict the caller: "v must not be 0", however, this feels incomplete, it should be valid to ask for the msb of 0. To address this, we must add more complexity. One possibility is to check v and reserve a return value for "no bit is msb", e.g. 32. This forces the user to rely on documentation in order to make the actual check against 32, a completely arbitrary value. Another is to use exceptions, but the overhead might be considered too much. A half-functional approach could be used as well, a struct with a validity field that can be set without branching e.g. ~v && 0xFFFFFFFF. This approach uses more memory, but forces the user to "unwrap" the value. While it is not ideal because the user can still unwrap invalid values it may remind the user that invalid values do exist. Bottom line, wouldn't it be cool if you could just select if you want the "incomplete" or the "complete" versions or as a consequence of the properties of the context in which the msb would be calculated a version is automatically selected and properly justified?